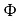) に比例する速度 
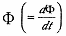で減衰する。このとき、系を記述する微分方程式は、実験方法及び理論解析
1. 実験方法
2. ラジカル減衰現象の数理
3. 非線型最小二乗法による数値解析
実験結果及び考察
1. 加熱前試料における ESR 信号のスペクトル挙動
2. 加熱による ESR 信号の挙動
3. 加熱によるラジカル減衰過程の定量化
食品の安全性はリスク分析によって評価される1)。今日では食品の安全性を確保するためにリスク評価やリスク管理さらにリスクコミュニケーションによって総合的に分析がなされている。
食品の安全性確保のための殺菌技術として最も注目されているものは放射線処理である。特にγ線照射は国際的に殺菌効果が認知され、頻用されている。既に、アメリカでは照射食品のリスク分析が行われており、最近の国際学会では照射食品のリスクコミュニケーションに及んだ研究報告2) がみられるようになっている。
電子スピン共鳴 （ESR） 法は広く放射線照射食品検知法3) として応用されている。ヨーロッパ連合では、公定法になっている。われわれは既に ESR 法について詳細な研究を行い EU 公定法を改良した検知法を提唱4) している。この改良 ESR 法を応用してセルロースを多く含む照射食品のラジカル検出5) について報告している。
本研究では、セルロースを多く含む食品 （胡椒と緑茶） にγ線照射処理し、ESR 法により加熱調理下でのラジカル挙動を解析した。ラジカルの加熱時の挙動を定量化することにより照射食品におけるリスク評価が可能になるか否かを検討した。
試料は既報5) と同じ市販胡椒と緑茶である。購入後直ちに冷蔵保存し、実験に供した。照射量は 50kGy とし、日本原子力研究所 （高崎研究所） にて実施した。加熱処理は実際の調理条件を想定してオーブン加熱を行った。加熱処理はサンプル 300mg をアルミニウムカップに秤量し、180℃ で 15 分程度余熱したオーブンで 1 分間間隔にて加熱して行った。ESR 測定条件は既報5) に準じた。
加熱によりラジカル量が減衰する現象を定式化した。ラジカルはある瞬間に存在するラジカル量 (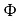) に比例する速度 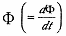で減衰する。このとき、系を記述する微分方程式は、
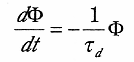 | (1) |
となる。ここで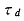 
はラジカル 1 個が減衰する時定数である。
初期条件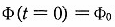 
のもと、(1) 式の微分方程式を変数分離法によって解くと、
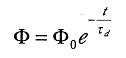 | (2) |
となる。
実測のデータにおいて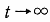 
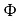における の値は必ずしも 0 とはならない。後述する最小二乗法によってデータ処理を行う場合この点が問題となる。この要件を満足すべく、境界条件 
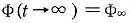を設定した。この条件下で次の解が得られる。
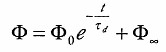 | (3) |
以下、(3) 式に基づき数値解析を行った。
(3) 式はラジカルの時間的消長を記述する。加熱下のラジカル減衰データはこの (3) 式によって、決定されるはずである。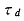 は減衰の時定数で、全体変化の 
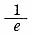に達するまでの時間として定義される恒定常数である。一般に 
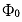と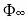 
は non-zero の値のために 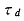を厳密に求めるには非線型最小二乗法を用いなければならない6)。
誤差の二乗和は、
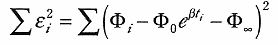 | (4) |
である。ここで、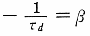
とおいた。
二乗和を最小とする 、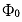
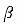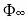、 は、
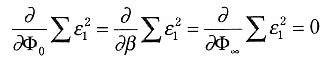 | (5) |
を満足する。
よって、
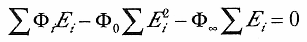 | (6.1) |
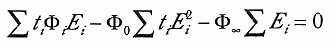 | (6.2) |
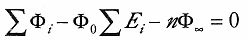 | (6.3) |
が得られる。ここで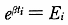 
とおいた。
(6.2) 式より 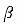が求められれば、(6.1) 式と (6.3) 式より容易に 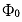と 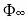が求められる。従って非線型最小二乗法に必要な初期値は 
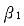のみ定めれば十分である。初期値 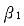は t の間隔 (
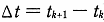) が一定であるから Patterson の式6) を用いて
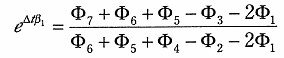 | (7) |
とした。これにより 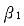が求められる。
(6.2) 式の左辺を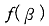 
とおくと、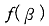 の一階微分 
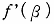は、
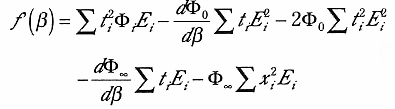 | (8) |
となる。ここで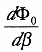 
と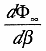 
は (6.1) 式と (6.3) 式より求めることができる。
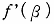が求まれば下記の Newton 法
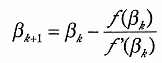 | (9) |
により有効数字の範囲内で 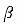を決定できる。
胡椒やお茶に発現する ESR 信号は 4 成分であった。即ち、g = 2.0 における有機フリーラジカル、g = 2.0 を中心とする六本線である Mn2+ による超微細構造線、g = 4.0 の Fe3+、及び照射試料に特有の一対の信号であった。これらは既報の結果5) と本質的に同一であり胡椒とお茶での ESR 信号スペクトル挙動に差異は見られなかった。
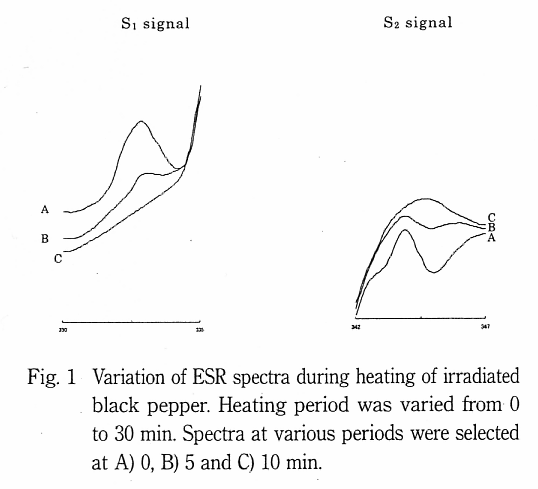
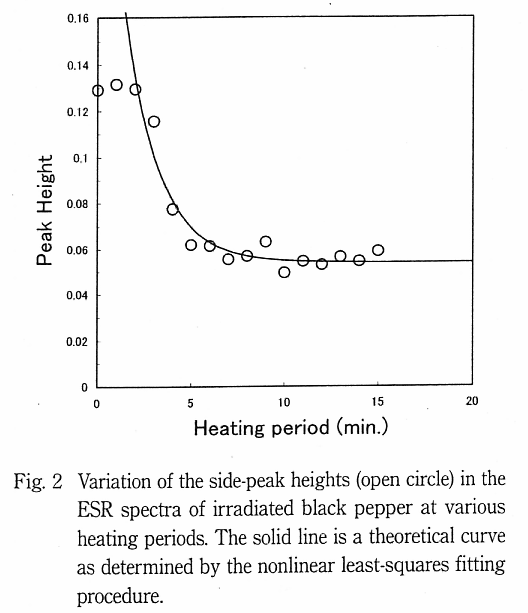
Fig. 1 に加熱処理時の照射黒胡椒で観測されたサテライト信号 (Ref. 5 中の Fig. 5 の S1 及び S2 を参照) の加熱時の挙動を示す。A で示した信号は加熱前にはシャープな信号であった。しかし、5 分及び 10 分加熱では顕著に信号強度が減少した。この現象について非線型最小二乗法を用いて解析した。ラジカル量 は (2) 式で記述される。(2) 式に基づき最小二乗法を適用すると、Fig. 2 の実線で描く最適曲線が得られた。
0 〜 15 分までの照射黒胡椒において値は 4.2 分となった。お茶では同様に解析すると値は 3.0 分であった。
 |
 |
本研究からγ線照射食品では加熱時にサテライトシグナルが減少するものの一定値に収束することが確認された。非線型最小二乗法の採用により、より信頼性の高い結果を得ることができた。回帰分析を用いて線型に変換するのではなく、直接、非線型最小二乗法を利用して数値解析を行った。非線型最小二乗法は、線型と比較して計算量が増加するが、求められる数値の信頼性は高い。非線型最小二乗法を用いた数値解析を行うことによって、加熱によるラジカル減衰の挙動について、恒定常数が正確に決定できることがわかった。しかし、セルロースを多く含む食品であっても食品の種類により時定数は異なることが示された。照射食品における τe の相互比較によって、加熱調理時の照射食品の厳密なるリスク評価が可能となると考えている。
1) http://www.maff.go.jp/
2) Torno M. : Education, The key to consumer acceptance of irradiated foods, International meeting on radiation processing, 115 (2003).
3) Raffi J. and Stocker P. : Electron paramagnetic resonance detection of irradiated foodstuffs, Appl. Magn. Reson., 10, 357-373 (1996).
4) Ukai M. and Shimoyama Y. : Free radicals in irradiated pepper, An electron spin resonance study, Appl. Magn. Reson., 24, 1-11 (2003).
5) 安部あいか他 : 電子スピン共鳴分光法によるセルロースを多く含んだ照射食品のラジカルの検出, 食品照射, 38, 1-5 (2003).
6) Snedecor G. W. and Cochran W. G. : 統計的方法 原書第6版, 畑村又好他共訳, 433-438, 岩倉書店 (1975).
（2004 年 6 月 2 日受理）
|
|